Chapter 7: Counterfactual Explanations

This chapter deals with further local analyses. First, counterfactuals are examined which search for data points in the neighborhood of an observation that lead to a different prediction.

§7.01: Counterfactual Explanations (CE)

• Suppose there exists a black-box model that takes in a loan applicant as an input \(\mathbf{x}\) (age, gender, loan_amount, purpose, etc) and determines whether the loan should be approved or rejected. Then given a decision, we may want to understand why the decision was reached.
• For this particular example, it could be useful to look into why the loan was rejected in particular and what needs to be different such that the loan is approved. For all other variables being equal, if changing race or gender changes the outcome of the loan application then, one would consider such a black-box model to be biased.
• Counterfactual Explanations aim to create such explanations by asking the question “How should x be changed so that the loan application is accepted?”.

• Formally, we aim to find a hypothetical input \(\mathbf{x'}\) close to the data point of interest \(\mathbf{x}\) whose prediction equals a user-defined desired outcome \(y'\):

  \[\mathbf{x'} \approx \mathbf{x} \text{ such that } f(\mathbf{x'}) = y' \text{ and distance } d(\mathbf{x, x'}) \text{ is minimal.}\]

• This can be thought of an optimization problem with two objects (one minimizing the loss between desired & predicted output; the other minimizing the distance between the point of interest and new data point):

  \[\operatorname{argmin}_{\mathbf{x'}} \lambda_1 o_{target}(\hat{f}(\mathbf{x'}, y')) + \lambda_2 o_{proximity}(\mathbf{x', x})\]
  More on $o_{target}$ and $o_{proximity}$

  1. Distance in target space $ o_{target} $: $ L_1, L_2 $, 0-1 Loss, etc
  2. Distance in input space $ o_{proximity} $: Gower distance (when feature types are mixed): $$ \begin{align*} o_{\text{proximity}}(\mathbf{x}', \mathbf{x}) &= d_G(\mathbf{x}', \mathbf{x}) = \frac{1}{p}\sum_{j=1}^{p} \delta_G(x'_j, x_j) \in [0, 1], \quad \text{where} \\ \delta_G(x'_j, x_j) &= \begin{cases} \mathbb{I}\{x'_j \neq x_j\} & \text{if } x_j \text{ is categorical} \\ \frac{1}{\text{range of feature j}} \mid x'_j - x_j\mid & \text{if } x_j \text{ is numerical} \end{cases} \end{align*} $$

Extending the Opyimization Problem

We also extend this optimization problem by considering other objectives apart from proximity/distance in order to improve explanation quality like Sparsity and Plausibility.

1. Sparsity favours counterfactual data points that have fewer feature changes. i.e. the most “proximal” counterfactual data point could have all features changed. Sparsity would instead prefer “more distant” data points that have fewer feature changes.
   • This could be integrated into \(o_{proximity}\) by using the \(L_0\) or \(L_1\) norm.
   • Alternatively, include a separate objectivity measure (e.g. via \(L_0\) norm):
   \[o_{sparse} = \sum_{j=1}^{p} 1(x_j' \neq x_j)\]
2. Plausibility: The proposed data points should be realistic and not implausible (e.g. becoming unemployed and increase in income). Estimating the joint distribution is hard especially if the feature spaces are mixed. A common proxy is to ensure that the new proposed point lies in the data manifold. This is done by preferring points that not necessarily “most proximal” but “most proximal to the training data / data manifold”.
   • This done by using the measuring the Gower distance of the proposed point to the nearest data point in the training dataset.

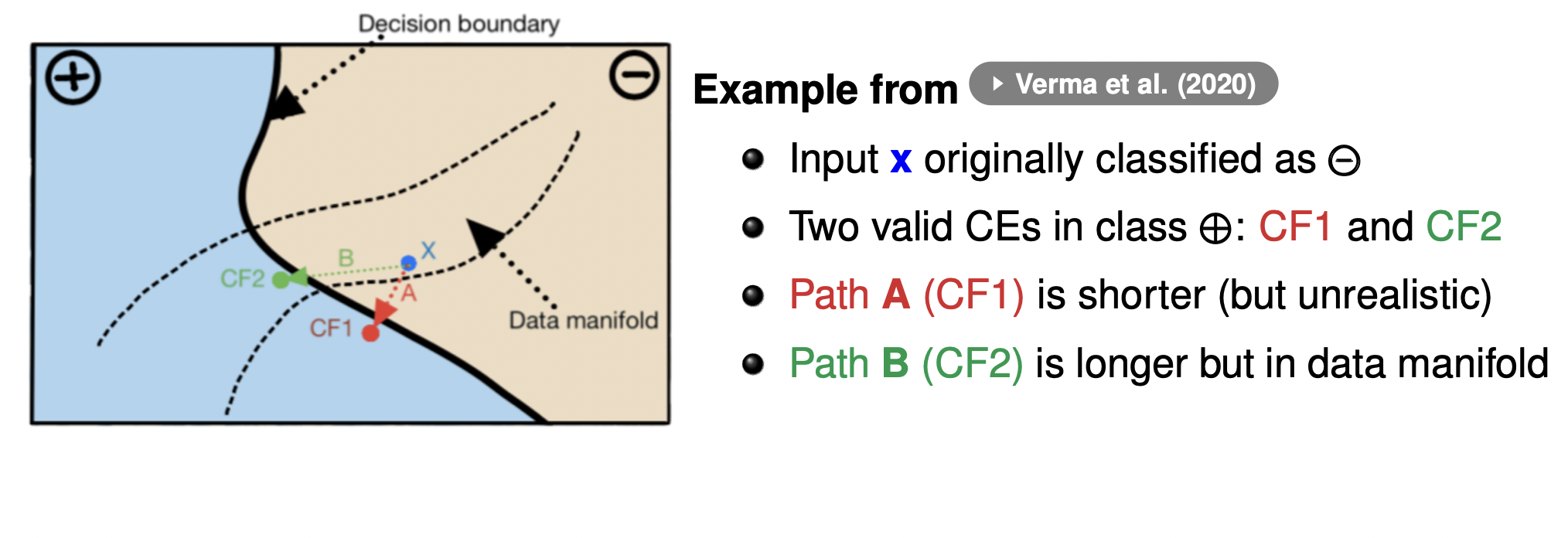
• The extended optimization problem is thus:

  \[\operatorname{argmin}_{\mathbf{x'}} \lambda_1 o_{target}(\hat{f}(\mathbf{x'}, y')) + \lambda_2 o_{proximity}(\mathbf{x', x}) + \lambda_3 o_{sparse}(\mathbf{x', x}) + \lambda_4 o_{plausible}(\mathbf{x', x})\]

• The solution to this optimization problem may not be unique and many equally good Counterfactual explanations may exist. This is known as the Rashomon effect. We could present all CEs for a given input (which requires human time and processing) or focus on one or few CEs (how to select these?). Black-Box models are generally non-linear and which could produce diverse CEs (one with increasing loan duration, and the other decreasing). This is potentially confusing to the end user.

CEs explain model predictions NOT real-world users .

---

§7.02: Methods & Discussion of CEs

Many methods exist to generate counterfactuals, they mainly differ in:

• Target: Most support classification (mostly for supervised learning tasks); few extend to regression
• Data type: Focus is on tabular data; little on text, vision, audio
• Feature Space: Some only handle numeric features; few extend to mixed types
• Objectives: From core goals like sparsity and plausibility to emerging aims such as fairness, personalization, and robustness
• Model Access: Methods range from model-specific (requiring model internals or access to gradients) to model-agnostic (using only prediction functions)
• Optimization: From gradient-based (differentiable models) and mixed-integer programming (linear models) to gradient-free methods (e.g., genetic algorithms)
• Rashomon Effect: Many methods return one CE, some diverse sets of CEs, others prioritize CEs, or let the user choose

First Optimization-Based CE Method

\[\operatorname{argmin}_{\mathbf{x'}} \max_\lambda \lambda (\hat{f}(\mathbf{x'}) - y')^2 + \sum_{j=1}^p \frac{\mid x_j' - x_j \mid}{MAD_j}\]

Where:

• The first term (\(o_{target}\)) ensures prediction change by increasing the weight \(\lambda\) and the second term (\(o_{proximity}\)) penalized deviations from \(\mathbf{x}\) rescaled by the Median Absolute Deviation of feature \(j\).
• Start with an initial \(\lambda\) and use a gradient-free optimizer like Nelder-Mead to minimize over \(\mathbf{x'}\). If the prediction constraint is not satisfied, increase \(\lambda\) and repeat. First achieve prediction validity, then minimize proximity.
• However this requires manual tuning of initial \(\lambda\), and has an asymmetric focus where early iterations are dominated by target loss. The proximity term is only defined for numerical features and additional objectives like sparsity, plausibility, diversity, etc are missing. Furthermore it returns only one CE and does not support diverse/ranked CEs.
• Multi-Objective CE: Instead of scalarizing/collapsing all objectives into a single objective, we can optimize all four objectives simultaneously. This avoids tuning the \(\lambda\)’s and returns a Pareto-optimal set instead (using NSGA-II for example) outputting diverse CEs representing different trade-offs between objectives.

Limitations and Pitfalls

• CEs only provide an illusion of model understanding by explaining ML decisions by pointing to few specific alternatives, reducing complexity but offering limited explanatory power
• The right similarity metric plays a crucial role in finding good CEs. (\(L_1\) can be reasonable for tabular data but not images for example).
• Model explanations are not easily transferable to reality because CEs provide insight into model NOT reality.
• CEs can disclose too much information and aid potential attackers.
• They are prone to Rashomon Effect as we don’t know how many CEs to show to the end user
• Focusing on actionable changes hinders fairness. The Plausibility constrain could restrict the potential CE to not change the users race/gender. However if only changing that changes the outcome then there is a bias in the model which is never revealed.
• Models can be gamed in such a way that the CEs are not faithful to underlying model